Definitions and conventions#
Information in this page is valid for spglib 1.8.1 or later. The definitions of transformation matrix and origin shift were different in the previous versions.
Space group operation and change of basis#
Basis vectors \((\mathbf{a}, \mathbf{b}, \mathbf{c})\) or \((\mathbf{a}_1, \mathbf{a}_2, \mathbf{a}_3)\)#
In spglib, basis vectors are represented by three column vectors:
in Cartesian coordinates. Depending on the situation, \((\mathbf{a}_1, \mathbf{a}_2, \mathbf{a}_3)\) is used instead of \((\mathbf{a}, \mathbf{b}, \mathbf{c})\).
Atomic point coordinates \(\boldsymbol{x}\)#
Coordinates of an atomic point \(\boldsymbol{x}\) are represented as three fractional values relative to basis vectors as follows,
where \(0 \le x_i < 1\). A position vector \(\mathbf{x}\) in Cartesian coordinates is obtained by
or
Symmetry operation \((\boldsymbol{W}, \boldsymbol{w})\)#
A symmetry operation consists of a pair of the rotation part \(\boldsymbol{W}\) and translation part \(\boldsymbol{w}\), and is represented as \((\boldsymbol{W}, \boldsymbol{w})\) in the spglib document. The symmetry operation transfers \(\boldsymbol{x}\) to \(\tilde{\boldsymbol{x}}\) as follows:
Transformation matrix \(\boldsymbol{P}\) and origin shift \(\boldsymbol{p}\)#
The transformation matrix \(\boldsymbol{P}\) changes choice of basis vectors as follows
where \(( \mathbf{a} \; \mathbf{b} \; \mathbf{c} )\) and \(( \mathbf{a}_\mathrm{s} \; \mathbf{b}_\mathrm{s} \; \mathbf{c}_\mathrm{s} )\) are the basis vectors of an arbitrary system and of a standardized system, respectively. In general, the transformation matrix is not limited for the transformation from the standardized system, but can be used in between any systems possibly transformed. It has to be emphasized that the transformation matrix doesn’t rotate a crystal in Cartesian coordinates, but just changes the choices of basis vectors.
The origin shift \(\boldsymbol{p}\) gives the vector from the origin of the standardized system \(\boldsymbol{O}_\mathrm{s}\) to the origin of the arbitrary system \(\boldsymbol{O}\),
Origin shift doesn’t move a crystal in Cartesian coordinates, but just changes the origin to measure the coordinates of atomic points.
A change of basis is described by the combination of the transformation matrix and the origin shift denoted by \((\boldsymbol{P}, \boldsymbol{p})\) where first the transformation matrix is applied and then origin shift. The points in the standardized system \(\boldsymbol{x}_\mathrm{s}\) and arbitrary system \(\boldsymbol{x}\) are related by
or equivalently,
A graphical example is shown below.
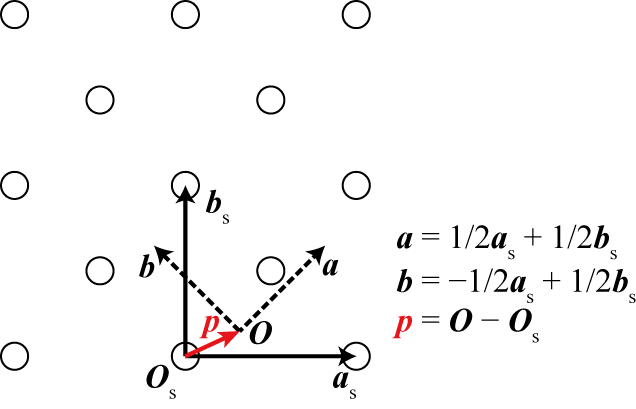
In this example,
Difference between rotation and transformation matrices#
A rotation matrix rotates (or mirrors, inverts) the crystal body with respect to origin. A transformation matrix changes the choice of the basis vectors, but does not rotate the crystal body.
A space group operation having no translation part sends an atom to another point by
where \(\tilde{\boldsymbol{x}}\) and \(\boldsymbol{x}\) are represented with respect to the same basis vectors \((\mathbf{a}, \mathbf{b}, \mathbf{c})\). Equivalently the rotation is achieved by rotating the basis vectors:
with keeping the representation of the atomic point coordinates \(\boldsymbol{x}\) because
The transformation matrix changes the choice of the basis vectors as:
The atomic position vector is not altered by this transformation, i.e.,
However the representation of the atomic point coordinates changes as follows:
because
Spglib conventions of standardized unit cell#
The standardization in spglib is achieved by a change of basis transformation. If idealization as shown below is further applied, the crystal can be rigidly rotated in Cartesian coordinates.
Choice of basis vectors#
Using the APIs spg_get_dataset,
spg_get_dataset_with_hall_number, or spg_standardize_cell, the
standardized unit cell is obtained. The “standardized unit cell” in
this document means that the (conventional) unit cell structure is
standardized by the crystal symmetry and lengths of basis
vectors. This standardization in spglib is not unique, but upto space
group operations and generators of Euclidean normalizer. Crystals are
categorized by Hall symbols in 530 different types in terms of 230
space group types, unique axes, settings, and cell choices. Moreover
in spglib, lengths of basis vectors are used to choose the order of
\((\mathbf{a}, \mathbf{b}, \mathbf{c})\) if the order can not be
determined only by the symmetrical conventions.
Transformation to the primitive cell#
In the standardized unit cells, there are five different centring types available, base centrings of A and C, rhombohedral ®, body centred (I), and face centred (F). The transformation is applied to the standardized unit cell by
where \(\mathbf{a}_\mathrm{p}\), \(\mathbf{b}_\mathrm{p}\), and \(\mathbf{c}_\mathrm{p}\) are the basis vectors of the primitive cell and \(\boldsymbol{P}_\mathrm{c}\) is the transformation matrix from the standardized unit cell to the primitive cell. \(\boldsymbol{P}_\mathrm{c}\) for centring types are given as follows:
The choice of transformation matrix depends on purposes. These transformation matrices above are just the spglib choices and may not be the best.
For rhombohedral lattice systems with the H setting (hexagonal lattice), \(\boldsymbol{P}_\mathrm{R}\) is applied to obtain primitive basis vectors, but for that with the R setting (rhombohedral lattice), no transformation matrix is applied because it is already the primitive cell.
Idealization of unit cell structure#
Spglib allows tolerance parameters to match a slightly distorted unit cell structure to a space group type with some higher symmetry. Using obtained symmetry operations, the distortion is removed to idealize the unit cell structure. The coordinates of atomic points are idealized using respective site-symmetries (Grosse-Kunstleve et al. (2002)). The basis vectors are idealized by forcing them into respective lattice shapes as follows. In this treatment, except for triclinic crystals, crystals can be rotated in Cartesian coordinates, which is the different type of transformation from that of the change-of-basis transformation explained above.
Triclinic lattice#
Niggli reduced cell is used for choosing \(\mathbf{a}, \mathbf{b}, \mathbf{c}\).
\(\mathbf{a}\) is set along \(+x\) direction of Cartesian coordinates.
\(\mathbf{b}\) is set in \(x\text{-}y\) plane of Cartesian coordinates so that \(\mathbf{a}\times\mathbf{b}\) is along \(+z\) direction of Cartesian coordinates.
Monoclinic lattice#
\(b\) axis is taken as the unique axis.
\(\alpha = 90^\circ\) and \(\gamma = 90^\circ\)
\(90^\circ < \beta < 120^\circ\).
\(\mathbf{a}\) is set along \(+x\) direction of Cartesian coordinates.
\(\mathbf{b}\) is set along \(+y\) direction of Cartesian coordinates.
\(\mathbf{c}\) is set in \(x\text{-}z\) plane of Cartesian coordinates.
Orthorhombic lattice#
\(\alpha = \beta = \gamma = 90^\circ\).
\(\mathbf{a}\) is set along \(+x\) direction of Cartesian coordinates.
\(\mathbf{b}\) is set along \(+y\) direction of Cartesian coordinates.
\(\mathbf{c}\) is set along \(+z\) direction of Cartesian coordinates.
Tetragonal lattice#
\(\alpha = \beta = \gamma = 90^\circ\).
\(a=b\).
\(\mathbf{a}\) is set along \(+x\) direction of Cartesian coordinates.
\(\mathbf{b}\) is set along \(+y\) direction of Cartesian coordinates.
\(\mathbf{c}\) is set along \(+z\) direction of Cartesian coordinates.
Rhombohedral lattice#
\(\alpha = \beta = \gamma\).
\(a=b=c\).
Let \(\mathbf{a}\), \(\mathbf{b}\), and \(\mathbf{c}\) projected on \(x\text{-}y\) plane in Cartesian coordinates be \(\mathbf{a}_{xy}\), \(\mathbf{b}_{xy}\), and \(\mathbf{c}_{xy}\), respectively, and their angles be \(\alpha_{xy}\), \(\beta_{xy}\), \(\gamma_{xy}\), respectively.
Let \(\mathbf{a}\), \(\mathbf{b}\), and \(\mathbf{c}\) projected along \(z\)-axis in Cartesian coordinates be \(\mathbf{a}_{z}\), \(\mathbf{b}_{z}\), and \(\mathbf{c}_{z}\), respectively.
\(\mathbf{a}_{xy}\) is set along the ray \(30^\circ\) rotated counter-clockwise from the \(+x\) direction of Cartesian coordinates, and \(\mathbf{b}_{xy}\) and \(\mathbf{c}_{xy}\) are placed by angles \(120^\circ\) and \(240^\circ\) from \(\mathbf{a}_{xy}\) counter-clockwise, respectively.
\(\alpha_{xy} = \beta_{xy} = \gamma_{xy} = 120^\circ\).
\(a_{xy} = b_{xy} = c_{xy}\).
\(a_{z} = b_{z} = c_{z}\).
Hexagonal lattice#
\(\alpha = \beta = 90^\circ\).
\(\gamma = 120^\circ\).
\(a=b\).
\(\mathbf{a}\) is set along \(+x\) direction of Cartesian coordinates.
\(\mathbf{b}\) is set in \(x\text{-}y\) plane of Cartesian coordinates.
\(\mathbf{c}\) is set along \(+z\) direction of Cartesian coordinates.
Cubic lattice#
\(\alpha = \beta = \gamma = 90^\circ\).
\(a=b=c\).
\(\mathbf{a}\) is set along \(+x\) direction of Cartesian coordinates.
\(\mathbf{b}\) is set along \(+y\) direction of Cartesian coordinates.
\(\mathbf{c}\) is set along \(+z\) direction of Cartesian coordinates.
Rotation introduced by idealization#
In the idealization step presented above, the input unit cell crystal structure can be rotated in the Cartesian coordinates. The rotation matrix \(\boldsymbol{R}\) of this rotation is defined by
This rotation matrix rotates the standardized crystal structure before idealization \(( \mathbf{a}_\mathrm{s} \; \mathbf{b}_\mathrm{s} \; \mathbf{c}_\mathrm{s} )\) to that after idealization \(( \bar{\mathbf{a}}_\mathrm{s} \; \bar{\mathbf{b}}_\mathrm{s} \; \bar{\mathbf{c}}_\mathrm{s} )\) in Cartesian coordinates of the given input unit cell.
Examples#
Throughout this section we are assuming that we are using a setup like:
Crystallographic choice and rigid rotation#
The following example of a python script gives a crystal structure of Br whose space group type is Cmce. The basis vectors \((\mathbf{a}, \mathbf{b}, \mathbf{c})\) are fixed by the symmetry crystal in the standardization. The C-centring determines the c-axis, and m and c operations in Cmce fix which directions a- and b-axes should be with respect to each other axis. This is the first one choice appearing in the list of Hall symbols among 6 different choices for this space group type.
# Mind that the a, b, c axes are given in row vectors here,
# but the formulation above is given for the column vectors.
lattice = [[7.17851431, 0, 0], # a
[0, 3.99943947, 0], # b
[0, 0, 8.57154746]] # c
points = [[0.0, 0.84688439, 0.1203133],
[0.0, 0.65311561, 0.6203133],
[0.0, 0.34688439, 0.3796867],
[0.0, 0.15311561, 0.8796867],
[0.5, 0.34688439, 0.1203133],
[0.5, 0.15311561, 0.6203133],
[0.5, 0.84688439, 0.3796867],
[0.5, 0.65311561, 0.8796867]]
numbers = [35,] * len(points)
cell = (lattice, points, numbers)
dataset = spglib.get_symmetry_dataset(cell)
print("Space group type: %s (%d)"
% (dataset['international'], dataset['number']))
print("Transformation matrix:")
for x in dataset['transformation_matrix']:
print(" %2d %2d %2d" % tuple(x))
print("Origin shift: %f %f %f" % tuple(dataset['origin_shift']))
This python script is saved in the file example.py. Then we get
Space group type: Cmce (64)
Transformation matrix:
1 0 0
0 1 0
0 0 1
Origin shift: 0.000000 0.000000 0.000000
No rotation was introduced in the idealization. Next, we swap a- and c-axes.
# Mind that the a, b, c axes are given in row vectors here,
# but the formulation above is given for the column vectors.
lattice = [[8.57154746, 0, 0], # a
[0, 3.99943947, 0], # b
[0, 0, 7.17851431]] # c
points = [[0.1203133, 0.84688439, 0.0],
[0.6203133, 0.65311561, 0.0],
[0.3796867, 0.34688439, 0.0],
[0.8796867, 0.15311561, 0.0],
[0.1203133, 0.34688439, 0.5],
[0.6203133, 0.15311561, 0.5],
[0.3796867, 0.84688439, 0.5],
[0.8796867, 0.65311561, 0.5]]
numbers = [35,] * len(points)
cell = (lattice, points, numbers)
dataset = spglib.get_symmetry_dataset(cell)
print("Space group type: %s (%d)"
% (dataset['international'], dataset['number']))
print("Transformation matrix:")
for x in dataset['transformation_matrix']:
print(" %2d %2d %2d" % tuple(x))
print("Origin shift: %f %f %f" % tuple(dataset['origin_shift']))
By this,
Space group type: Cmce (64)
Transformation matrix:
0 0 1
0 1 0
-1 0 0
Origin shift: 0.000000 0.000000 0.000000
We get a non-identity transformation matrix, which wants to transform back to the original (above) crystal structure by swapping a- and c-axes. The transformation back of the basis vectors is achieved by Eq. (6). Next, we try to rotate rigidly the crystal structure by \(45^\circ\) around c-axis in Cartesian coordinates from the first one:
# Mind that the a, b, c axes are given in row vectors here,
# but the formulation above is given for the column vectors.
lattice = [[5.0759761474456697, 5.0759761474456697, 0], # a
[-2.8280307701821314, 2.8280307701821314, 0], # b
[0, 0, 8.57154746]] # c
points = [[0.0, 0.84688439, 0.1203133],
[0.0, 0.65311561, 0.6203133],
[0.0, 0.34688439, 0.3796867],
[0.0, 0.15311561, 0.8796867],
[0.5, 0.34688439, 0.1203133],
[0.5, 0.15311561, 0.6203133],
[0.5, 0.84688439, 0.3796867],
[0.5, 0.65311561, 0.8796867]]
numbers = [35,] * len(points)
cell = (lattice, points, numbers)
dataset = spglib.get_symmetry_dataset(cell)
print("Space group type: %s (%d)"
% (dataset['international'], dataset['number']))
print("Transformation matrix:")
for x in dataset['transformation_matrix']:
print(" %2d %2d %2d" % tuple(x))
print("Origin shift: %f %f %f" % tuple(dataset['origin_shift']))
and
Space group type: Cmce (64)
Transformation matrix:
1 0 0
0 1 0
0 0 1
Origin shift: 0.000000 0.000000 0.000000
The transformation matrix is kept unchanged even though the crystal structure is rotated in Cartesian coordinates. The origin shift is different but it changes only the order of atoms, so effectively it does nothing.
Transformation to a primitive cell#
There are infinite number of choices of primitive cell. The transformation from a primitive cell basis vectors to the other primitive cell basis vectors is always done by an integer matrix because any lattice points can be generated by the linear combination of the three primitive basis vectors.
When we have a non-primitive cell basis vectors as given in the above example:
lattice = [[7.17851431, 0, 0], # a
[0, 3.99943947, 0], # b
[0, 0, 8.57154746]] # c
This has the C-centring, so it must be transformed to a primitive cell. A possible transformation is shown at Transformation to the primitive cell, which is \(\boldsymbol{P}_\mathrm{C}\). With the following script:
lattice = [[7.17851431, 0, 0], # a
[0, 3.99943947, 0], # b
[0, 0, 8.57154746]] # c
Pc = [[0.5, 0.5, 0],
[-0.5, 0.5, 0],
[0, 0, 1]]
print(np.dot(np.transpose(lattice), Pc).T) # given in row vectors
we get the primitive cell basis vectors (shown in row vectors):
[[ 3.58925715 -1.99971973 0. ]
[ 3.58925715 1.99971973 0. ]
[ 0. 0. 8.57154746]]
find_primitive gives a primitive cell that is obtained by
transforming standardized and idealized crystal structure to the
primitive cell using the transformation matrix. Therefore by this
script:
lattice = [[7.17851431, 0, 0],
[0, 3.99943947, 0],
[0, 0, 8.57154746]]
points = [[0.0, 0.84688439, 0.1203133],
[0.0, 0.65311561, 0.6203133],
[0.0, 0.34688439, 0.3796867],
[0.0, 0.15311561, 0.8796867],
[0.5, 0.34688439, 0.1203133],
[0.5, 0.15311561, 0.6203133],
[0.5, 0.84688439, 0.3796867],
[0.5, 0.65311561, 0.8796867]]
numbers = [8,] * len(points)
cell = (lattice, points, numbers)
primitive_cell = spglib.find_primitive(cell)
print(primitive_cell[0])
we get:
[[ 3.58925715 -1.99971973 0. ]
[ 3.58925715 1.99971973 0. ]
[ 0. 0. 8.57154746]]
This is same as what we manually obtained above. Even when the basis vectors are rigidly rotated as:
lattice = [[5.0759761474456697, 5.0759761474456697, 0],
[-2.8280307701821314, 2.8280307701821314, 0],
[0, 0, 8.57154746]]
the relationship of a, b, c axes is unchanged. Therefore the same transformation matrix to the primitive cell can be used. Then we get:
[[3.95200346 1.12397269 0. ]
[1.12397269 3.95200346 0. ]
[0. 0. 8.57154746]]
However applying find_primitive rigidly rotates automatically and
so the following script doesn’t give this basis vectors:
lattice = [[5.0759761474456697, 5.0759761474456697, 0],
[-2.8280307701821314, 2.8280307701821314, 0],
[0, 0, 8.57154746]]
points = [[0.0, 0.84688439, 0.1203133],
[0.0, 0.65311561, 0.6203133],
[0.0, 0.34688439, 0.3796867],
[0.0, 0.15311561, 0.8796867],
[0.5, 0.34688439, 0.1203133],
[0.5, 0.15311561, 0.6203133],
[0.5, 0.84688439, 0.3796867],
[0.5, 0.65311561, 0.8796867]]
numbers = [8,] * len(points)
cell = (lattice, points, numbers)
primitive_cell = spglib.find_primitive(cell)
print(primitive_cell[0])
but gives those with respect to the idealized ones:
[[ 3.58925715 -1.99971973 0. ]
[ 3.58925715 1.99971973 0. ]
[ 0. 0. 8.57154746]]
To obtain the rotated primitive cell basis vectors, we can use
standardize_cell as shown below::
lattice = [[5.0759761474456697, 5.0759761474456697, 0],
[-2.8280307701821314, 2.8280307701821314, 0],
[0, 0, 8.57154746]]
points = [[0.0, 0.84688439, 0.1203133],
[0.0, 0.65311561, 0.6203133],
[0.0, 0.34688439, 0.3796867],
[0.0, 0.15311561, 0.8796867],
[0.5, 0.34688439, 0.1203133],
[0.5, 0.15311561, 0.6203133],
[0.5, 0.84688439, 0.3796867],
[0.5, 0.65311561, 0.8796867]]
numbers = [8,] * len(points)
cell = (lattice, points, numbers)
primitive_cell = spglib.standardize_cell(cell, to_primitive=1, no_idealize=1)
print(primitive_cell[0])
then we get:
[[3.95200346 1.12397269 0. ]
[1.12397269 3.95200346 0. ]
[0. 0. 8.57154746]]
which is equivalent to that we get manually. However using
standardize_cell, distortion is not removed for the distorted
crystal structure.
Computing rigid rotation introduced by idealization#
In spglib, rigid rotation is purposely introduced in the idealization step though this is unlikely as a crystallographic operation.
The crystal structure in the following script is the same as shown above, which is the one \(45^\circ\) rotated around c-axis:
# Mind that the a, b, c axes are given in row vectors here,
# but the formulation above is given for the column vectors.
lattice = [[5.0759761474456697, 5.0759761474456697, 0], # a
[-2.8280307701821314, 2.8280307701821314, 0], # b
[0, 0, 8.57154746]] # c
points = [[0.0, 0.84688439, 0.1203133],
[0.0, 0.65311561, 0.6203133],
[0.0, 0.34688439, 0.3796867],
[0.0, 0.15311561, 0.8796867],
[0.5, 0.34688439, 0.1203133],
[0.5, 0.15311561, 0.6203133],
[0.5, 0.84688439, 0.3796867],
[0.5, 0.65311561, 0.8796867]]
numbers = [35,] * len(points)
cell = (lattice, points, numbers)
dataset = spglib.get_symmetry_dataset(cell)
print("Space group type: %s (%d)"
% (dataset['international'], dataset['number']))
print("Transformation matrix:")
for x in dataset['transformation_matrix']:
print(" %2d %2d %2d" % tuple(x))
print("std_lattice_after_idealization:")
print(dataset['std_lattice'])
we get
Space group type: Cmce (64)
Transformation matrix:
1 0 0
0 1 0
0 0 1
std_lattice_after_idealization:
[[7.17851431 0. 0. ]
[0. 3.99943947 0. ]
[0. 0. 8.57154746]]
From Eq. (6), the standardized basis vectors
before idealization \(( \mathbf{a}_\mathrm{s} \; \mathbf{b}_\mathrm{s}
\; \mathbf{c}_\mathrm{s} )\) is obtained by (after import numpy as np)
std_lattice_before_idealization = np.dot(
np.transpose(lattice),
np.linalg.inv(dataset['transformation_matrix'])).T
print(std_lattice_before_idealization)
which is (in row vectors)
[[ 5.07597615 5.07597615 0. ]
[-2.82803077 2.82803077 0. ]
[ 0. 0. 8.57154746]]
This is different from the standardized basis vectors after idealization \(( \bar{\mathbf{a}}_\mathrm{s} \; \bar{\mathbf{b}}_\mathrm{s} \; \bar{\mathbf{c}}_\mathrm{s} )\). Unless this crystal structure is distorted from the crystal structure that has the ideal symmetry, this means that the crystal was rotated rigidly in the idealization step by
where \(\boldsymbol{R}\) is the rotation matrix. This is computed by
R = np.dot(dataset['std_lattice'].T,
np.linalg.inv(std_lattice_before_idealization.T))
print(R)
and we get
[[ 0.70710678 0.70710678 0. ]
[-0.70710678 0.70710678 0. ]
[ 0. 0. 1. ]]
This equals to
with \(\theta = -\pi/4\) and \(\det(\boldsymbol{R})=1\) when
no distortion. dataset['std_rotation_matrix'] gives
approximately the same result:
[[ 0.70710678 0.70710678 0. ]
[-0.70710678 0.70710678 0. ]
[ 0. 0. 1. ]]
In summary,
The atomic point coordinates in \(( \bar{\mathbf{a}}_\mathrm{s} \; \bar{\mathbf{b}}_\mathrm{s} \; \bar{\mathbf{c}}_\mathrm{s} )\) are simply obtained by Eq. (8) since the rotation doesn’t affect them.